Updates added 22 January 2004
John Boozer
and Guenter Stertenbrink both
found gorgeous embeddings of the F64 graph.
I finally tracked down the persons responsible for notating the second
graph as [23,-11,-29,25,-25,29,11,-23]8. In addition
to HSM Coxeter and Roberto Frucht, Joshua Lederberg - the winner of the
1958 Nobel Prize in Physiology and Medicine -- did a large study
(pdf) of graphs notated in a similar way. Doctor Lederberg's complete
works are available online. Another graph that deserves a
nice picture is the Hoffman-Singleton
graph.
Jens Kruse Andersen: Hans Rosenthal
and I have found a prime gap
of 1001548 between two probabilistic primes (prp's) with 43429
digits. The logarithm of the primes is 99997 so the gap is 10.02
times the "typical" gap by the prime number theorem. I think that
regardless of relative size, this is the first known prime "megagap"
with identified (probabilistic) primes as gap ends.
Xah Lee has put together a page on Algorithmic
Mathematical Art.
Dick Hess modified a puzzle first posed by
E.K. Chapin in 1927. You have 2 mugs, a water supply, and a
packet of instant coffee which when dissolved in one cup produces
coffee of strength 100%. Your task is to fix coffee as
requested. You may fill or transfer liquid and may, at any time,
empty the entire coffee packet into a mug. Send Answers.
Material added 13 January 2004
The Wolfram Functions Site has
been vastly expanded. More than a hundred volumes worth of
function information.
A highlight is the 10,000+ visualizations of every function, in many
different ways. Code for all visualizations is provided. My
latest MAA column talks about it more.
Harvey Heinz has updated his page about magic cubes.
I was completely unaware of Frankenstein's Cube.
My last MAA column of
December 2003 talks
about Cubic
Symmetric Graphs. I'm quite proud of my version of the
Coxeter Graph, there -- I made it the logo for the Mathpuzzle Yahoo Group.
Erich Friedman has updated his page of Sequential Domino Packings. His solution for 18 dominoes might not be minimal -- can you fit these into a 65x65 square? Send Answer (if one exists) Smallest packings for both 23 and 24 sequential dominoes might also be very tricky to find. Robert Reid, Erich Friedman, Minami Kawasaki, and myself have all been busy finding solutions -- see Sequence A005842. Solutions for 16, 21, 34, 46, 54, 56, 60, 62, 63, 65, and 76 can be found in this zip. Minami Kawasaki has put together a page about sequential squares.

Francis Heaney: I review the new Jell-O
Checkers snack packet on my blog today. It has many flaws, and I
was hoping someone would step forward to help analyze how they affect
the game. [Ed - I expect a Zillions expert will crack this in
hours. Send Answer.]
Cihan Altay: PQRST 08 Puzzle Competition
starts on January 17th Saturday at 20:00 (GMT+02). You'll have one week
to solve and rate 10 puzzles.
Yasutoshi Kohmoto: 2004^6 =
3959307^3 + 1393389^3 + 1494^3 = 3848682^3 + 1980119^3 + 27889^3
Karl Scherer has greatly expanded his WireWorld results,
with help from Nyles Heise. Pentomino Odd
Pairs (by Livio Zucca) is well worth a look -- can you find a shape
made with an odd number of either I or V pentominoes?
A noted game and puzzle creator has
recently been harassed
for having an almanac. He'll be attending the MIT Mystery
Hunt this week. Warm-up
puzzle.
Material added 1 January 2004

Livio Zucca has created a page with
various pentomino
and tetromino challenges. For example, find a shape that can be
split into either I or T tetrominoes, but none of the others.
George Jelliss has release Issue 30 of the
Games and Puzzles
Journal. The bound volumes he offers are a nice prize, and
many of the puzzles there are quite nice. I especially like problems 64
and 65.
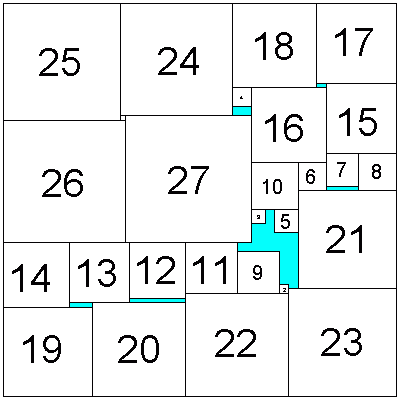
Packing squares in squares. Robert
Reid sent my a nice Christmas Present -- squares 1-27 packed into the
smallest possible square. I played around with the problem of
1-25 in the smallest square. One of my best efforts is shown
here. I don't have a proper 8 packed in here. However, I
could fit in 3 4x8 rectangles and everything else into the 75x75
square. Paul Cleary sent me a solution for 1-25 packed into a 76x76
square, but he believes (as I do) that 75x75 must have a solution.
Erich Friedman is presenting a slightly different take on Squares in Squares
this month at Math Magic.

A puzzle by Marek Penszko of Poland.
It's a division problem. Answer.
Dave Millar: I was inspired by the room puzzles by
Erich Friedman, and made one of my own creation. 3 room, all of 8
squares. From each number, you can see that number of spaces in any
direction; up, down, left, or right. Answer.

Material added 23 December 2003
Cletus Emmanuel has found that (2^148330+1)^4 - 2 is a
probable
prime. That makes it the largest known probable prime on the
Henri Lipchitz Probable
Prime List. Seventeenorbust.com
reports that 5359•2^5054502+1 is now the 4th largest proven
prime.
Dave Millar has sent me several nice puzzles. In the
Pento puzzle, rearrange the given double size pentominoes so that the
squares in the grid represent the number of smaller pentominoes in each
one. (Answer) I also like this logo
he did for me. In the Bird puzzle (solution),
the bird must be divided into
5 identical shapes, not necessarily of the same size.



Colonel Sicherman, on the Logical
Hats problem: "After one logician identifies his number, can the
other two always identify theirs immediately? I have not found a
counterexample." Answer.
NetLogo
2.0 is available for download. This is the programming
language of Turning Turtles fame. There are many excellent and
instructive programs built in.

I'm trying to learn a little TeX. I didn't make
much headway until I tried out a combination of the winedt shell and MiKTeX.
My latest two Math Games columns are Domino
Graphs and Superflu
Modeling. Here's a rainbow PDF
version of the Petersen Graph I did as an experiment, after getting
some kind words for the first article.
Erich Friedman: Find positive integers A, B, C, D, and
E all less than 100 so that A2 + B2 + C2
= D2 + E2 and A3 + B3
+ C3 = D3 + E3. Answer and Solvers.
Johan de Ruiter: "Last night I was wondering whether
any integer can be written as a linear combination of a finite number
of noninteger squareroots of integers where all coefficients are
integers. Maybe it's trivial, but I wasn't able to find a solution
yet." I wasn't able to find a trivial proof either, beyond proofs
for 2 or 3 square roots. Is there a clever impossibility proof? Answer.
The square of 40081787109376 starts
16065496578813... how does it end?
Material added 13 December 2003
My latest Math Games column
deals with Integer
Sequences.
Des MacHale of University College Cork found a way to fit squares of
size 1-24 in a 43×115 rectangle. All rectangles smaller than
54×91
have been shown to be unsolvable by Patrick Hamlyn. Thus, the necessary
excess required for a rectangular packing of squares 1-24 ranges from
14 to 45 (below). I thought this might make a nice puzzle -- treating
the blue areas below as holes, divide the 43×115 rectangle below
into 24 squares. Slide your mouse over the image to see the
solution. For 1-22, rectangles smaller than 53×72 are
unsolvable. (Patrick Hamlyn: The squares 1-22 into a rectangle: I
just finished searching 53*72, no solutions after 589.5 hours.) For
1-23, 61×71 might be possible, or maybe
62×70,
but probably something larger is needed. As a warm-up puzzle,
here's a beauty: Divide an 11×11 square into 11 squares of size
2-5. See my Square
Packing column for more.

Des MacHale's packing of squares 1-24 in a 43×115 rectangle.
Nyles Heise (nylesheise at yahoo.com) fit a 32-bit WireWorld
multiplier into a 22×93 rectangle.  Yes, that is a very tiny
multiplication program. You can see his
notes, or his MCL representation.
(Two Updates: Input 1's,
and Output 1's) You can
download MCell from Mirek's
site. In hexadecimal, the below calculates EF4E75E7 EFA03229 =
DFFFFFFFFFF7FFFF in 8116 cycles. See the Output 1's file for an
expanded MCell version.
Yes, that is a very tiny
multiplication program. You can see his
notes, or his MCL representation.
(Two Updates: Input 1's,
and Output 1's) You can
download MCell from Mirek's
site. In hexadecimal, the below calculates EF4E75E7 EFA03229 =
DFFFFFFFFFF7FFFF in 8116 cycles. See the Output 1's file for an
expanded MCell version.
#SG
..............................................................................................
#SG
..OOOOOOOOOOOOOOOOOOOOOOO.O.O...O.OOOO.OOOOOOOOOO.OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO..
#SG
.O.......................OOO.*OOOO....O..........O..........................................O.
#SG
..OOOOOOOOOOOOOOOOOOOOO...O.o...O.O..OOO..O...OOO..OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO..
#SG
.......................O.O.....O...O..O..*.O.O....O...........................................
#SG
..OOOOOOOOOOOOOOOOOOOOO..O....O..OO..OOOO*o...OOO..OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOo*OOo*OOo..
#SG
.O.......................O...O..O...O.O....*.....O..........................................*.
#SG
..OOOOOOOOOOOOOOOOO...O..O..O...O...O...OO..OO.*..*oOO*oOO*oOOOOOOOOOO*oOO*oOO*oOO*oOOOOOO..O.
#SG
...................O.O.O.OOO....O....O.O..O...O*o.........................................*.O.
#SG
..OOOOOOOOOOOOOOOOO..O.O..O...O..O....OOO.O.O..*.O*o.O*oOO*oOOOOOO*oOO*oOO*oOO*oOO*oOOOO..o.O.
#SG
.O...................O.O..OOOOOOO....O.*...OOOO.....O...................................O.O.O.
#SG
..OOOOOOOOOOOOOOOOO..O.O.O....O...*...o.....O......o..*OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOo*O..O.O.
#SG
...................O.O.O.O.O.OO.Oo.O.OOO..OO.......*.o....................................O.O.
#SG
..OOOOOOOOOOOOOOOOO..O..OOOOO..OO.O...O..o.O.oO..o.O..OO*oOOOOOOOOOO*oOOOOOO....Oo*OOo*OOO..o.
#SG
.O...................O...*.O.O..OOO....O*...*..*ooO.........................O..O............*.
#SG
..OOOOOOOOOOOOOOOO...O...o....O..O.............o.o.OOOOOOOOo*OOOOOOo*OOOOOOO....*oOOOOOOOO..O.
#SG
..................O..O..O.*....O.O.....*OOo*OOO...........................................O.O.
#SG
..OOOOOOOOOOOOOOOO..OO...O..OOO..O....o.........o*OOo*OOOo*OOo*OOo*OOo*OOo*O...O...o*OOo*O..o.
#SG
.O.................O.OO....O.....O...O....OOo*OO............................O.O.*.O.........*.
#SG
..OOOOOOOOOOOOOOO..O...O..OOO.O.OOO.O..O**.......O*oOO*oOO*oOO*oOO*oOO*oOO..oooo...O*oOOOO..O.
#SG
.................O.O..OOO..O.OOO.O..*.O..o......O.........................*..O..*.........O.O.
#SG
..OOOOOOOOOOOOOOO..O.O.O.OO.O.O..o.O*OO.O.O......o*OOo*OOo*OOo*OOo*OOo*OO..oOOO.O..o*OOOOO..o.
#SG
.O.................O.O..........*.O.*.OO...O.............................o...O..O.O.........*.
#SG
..OOOOOOOOOOOOOOOOO...OOOOOOOOOO.O......*oO.*oOO*oOO*oOO*oOO*oOO*oOO*oOO*.....*o...OOOOO*oOO..
#SG
..............................................................................................
CHESS MAZE by Mark J. P. Wolf (mark.wolf at cuw.edu): "I’ve always
admired the rich possibilities in the simplicity of the chessboard, and
tried to capture this in the Chess maze. How the maze
works: Starting with the White Queen at a8, capture your way to
the White King at h1. Pieces capture as they do in chess (except
pawns, which can
capture one square diagonally in any
direction), and pieces can only
capture pieces of the opposite color. However, once a capture is
made your piece becomes the type of piece that was just captured (and
moves accordingly on the next move) and all moves must end in a
capture. Pieces that are captured are removed from the board, so
the number of pieces on the board gradually decreases. To keep
track of which pieces are removed, I recommend either crossing out the
captured pieces, so as to indicate which squares are empty and can be
passed over later in the maze. (For an easy warm-up, try
capturing the black queen in five moves, or the black pawn at a1 in
nine moves). A unique feature of the maze is
that as pieces are captured and removed, new pathways open up that were
previously unavailable, making the maze fairly difficult to work
backwards." Answer and Solvers. Picture of Solution. Doug
Orleans created an
applet for this puzzle.

Brian Silverman did a Google
search on 5-digit numbers, and
discovered that 17839 is the most unpopular number on the
internet. I'm trying to help the number, since 17839 ×
19813 × 237877 × 11893969 = 1021
- 9. It's also a factor of 35! + 11.. Does this number have
anything else going for it? Send
17839 factoids. Livio Zucca is searching for pento-tetra-tri
solutions. Jorge Mireles has expanded his page on Poly2ominoes.
Peter Esser has found a way to pack the Sliced
Heptiamonds into a rectangle.

Jim Propp recently gave a talk to the theory group at Microsoft
Research entitled "Random walk
and random aggregation, derandomized", which Microsoft has made
available to the outside world. Watching the video/demo is
probably the quickest and most pleasant way to find out the current
state of knowledge about these models.
Slouching Towards Bedlam won the Interactive Fiction Competition. The solutions I received for Borromean Rings are great.
Material added 4 December 2003
RSA-576 has been factored by the programming team of J. Franke, T. Kleinjung, P. Montgomery, H. te Riele, F. Bahr, D. Leclair, Paul Leyland and R. Wackerbarth. Institutions involved include Bonn University, the Max Planck Institute, the Experimental Mathematics Institute in Essen, CWI, NFSNET, and Microsoft Research. For this development and application of the GNFS algorithm, they will split $10,000.00. NSFNET (Number Field Sieve Net) just happens to be recruiting, if you'd like to join the effort to factor 2^811 - 1. They recently factored 2^757-1.
188198812920607963838697239461650439807163563379417382700763356422988859715234665485319
060606504743045317388011303396716199692321205734031879550656996221305168759307650257059
=
398075086424064937397125500550386491199064362342526708406385189575946388957261768583317
×
472772146107435302536223071973048224632914695302097116459852171130520711256363590397527.
Material added 2 December 2003
A few years ago, Michael Shafer was visiting here. Michael: "Yes, yes, it's all true! I came across mathpuzzle.com some time in 2000 and bookmarked it to check out the puzzles you came out with every week as well as the interesting links. www.mersenne.org was one of them and you can see what happened. Thank you for leading me to Al Zimmerman's contests, the WPC qualifiers, and Theodore Gray's periodic table and fun with sodium as well. The occasional challenges are also fun to spend a few minutes (or sometimes more) pondering. Keep up the great work!" If you check out the mersenne.org link, you'll see that Michael Shafer helped to discover the world's largest prime, 220996011-1. Many congratulations, Michael! You can see more at mathworld.wolfram.com.
More record setting news from Lance Gay: " I just saw your new Square Packing page at maa.org. I have improved solutions to 198, 205, 206, 253, 258, and 259." My next goal is to correct my graphic of primitive quilts.
198-21
{{106,92},{12,13,19,48},{2,9,1},{14},{92,16},{19},{9},{3,11},{28},{20,10},{58},{48}}
205-21
{{112,93},{22,23,48},{93,16,3},{13,12},{11,12},{11,11,1},{29},{13},{19,3},{64},{48}}
206-21
{{113,93},{23,25,45},{93,17,3},{19,7},{5,20},{12},{12,5},{7,26,3},{68},{19},{45}}
253-22
{{141,112},{27,28,57},{1,9,16,1},{1},{29},{112,23,7},{16},{16},{32,7},{2,84},{25},{57}}
258-22
{{142,116},{25,33,58},{1,12,12},{116,27},{4,4,25},{12,20},{4,8},{31},{27,1},{84},{58}}
259-22
{{142,117},{25,34,58},{117,31,19},{10,24},{15,14},{28,3},{12,84},{9,9},{16,2},{14},{58}}
Material added 1 December 2003
Two more new columns at my MAA column, Math Games. First, a treatise on Multistate Mazes. Next, a synopsis of the current knowledge of Square Packings, in particular the case of Mrs. Perkins's Quilt. For the latter, Richard Guy and I tried to create a list of Primitive Optimal Quilts, and already a number of mistakes are apparent. Can you find the three quilts that aren't primitive, and the primitive quilt that can be derived from one of them? Yesterday, Richard K Guy learned, demonstrated, then stressed to me how important the primitive quilts are for solving the general problem. A correct list of primitive quilts up to size 100 is needed. Write me if you discover a patch in the solution for Mrs. Perkins's Quilt. I can well imagine a high-schooler picking one of the primitive squares, tracing through the build-up process, and becoming permanent listed in the problem's history. A great resource for this is squaring.net.
Slightly too late for the multistate column is Perl Code for Logic Mazes. As a possible gift, Robert Abbott has about 20 copies of each of his wonderful maze books left -- see his site for information. Even raarrer, William Waite has ten copies of his Camera Conundrum puzzle. It's an incredibly clever secret-opening box. It won at the last International Puzzle Design competition. Speaking of that ....
The 4th IPP Puzzle Design Competition has started. Established three years ago to promote and recognize innovative new designs of mechanical puzzles, the annual IPP Puzzle Design Competition will be held in conjunction with IPP24 in Tokyo. The competition is open to designs made public between July, 2002 and July, 2004. Entry Deadline: June 30, 2004. Judging at IPP: July 30 - August 1, 2004. Awards at IPP: August 1, 2004. Complete rules and information are at the IPP Puzzle Design Competition web site, part of John Rausch's PuzzleWorld. The third competition completed in August with judging and awards at IPP23 in Chicago, USA. It was a great success, with 52 designs participating. Lee Krasnow's Clutch Box won the Puzzlers' Award; and Mineyuki Uyematsu's Cube in Cage 333 won the judging committee's Grand Prize.
Another gift possibility -- I have a domino cards game out, Auf & Ab. The link will take you to Funagain Games. It's basically a nicely improved set of double-9 domino cards, perfect for playing my game Ups and Downs. If you want a book, I'm still fascinated by Mathematical Constants by Steven Finch. Easier reading is Dudeney's Amusements in Mathematics, which was my first puzzle book.
Routewords is an interesting combination of graph theory and wordplay. Ross Eckler tackled this problem back in 1980 -- find a non-planar word. Also at Word Ways, some of the challenges are worth a look.
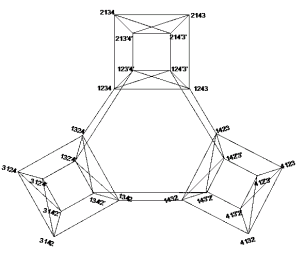
Inspired by Bill Cutler's solution, Fan Chung and Ron Graham have done a detailed combinatorical analysis of the Archimedean Stomachion. It turns out the solutions have a fantastic amount of symmetry. Archimedes could have found all of this easily ... and he may have!
Dick Hess: The Logical Hats Puzzle. Logicians A, B and C each
wear a hat with a positive integer on it such that the number on one
hat is the sum of the numbers on the other two. They can see the
numbers on the other two hats but not their own. They are given
this information and asked in turn if they can identify their
number. In the first round A, B and C each in turn say they don't
know. In the second round A is first to go and states his number
is 50. What numbers are on B and C? Answer
and Solvers. Jonathan Welton: I was delighted to see an old puzzle
of mine doing the rounds (Logical Hats Puzzle). This was originally
published in the Sunday Times magazine as puzzle number
1814, and was reprinted in a collection of these puzzles,
Brainteasers by Victor Bryant in 2002 - highly recommended if you like
tough puzzles.
A 2000 year old icosahedron is available for auction at Christie's. More glimpses of ancient math are stored at the Vatican. I recently refound a long-lost link -- Monty Hall's take on the Monty Hall puzzle.
Older material
Anyone can subscribe to my moderated mailing list
at http://groups.yahoo.com/group/mathpuzzle/.
I announce updates to this site via that list.
07Oct03-18Nov03
25Aug03-30Sep03
06Jul03-17Aug03
01Apr03-29Jun03
25Dec02-26Mar03
29Oct02-13Dec02
03Sep02-21Oct02
16Jul02-26Aug02
13May02-09Jul02
04Mar02-06May02
05Dec01-25Feb02
19Aug01-04Dec01
17Feb01-05Aug01
02Jun00-11Feb01
More
Math
Puzzle Pages
Awards,
Book Recommendations, Chaos
Tiles, Characteristic Polynomial, ChebyshevU, Chromatic
Number of the Plane, Coin Weighing, Complex Numbers, Connecting
Dots, Crosswords, Digital
Sums, Dissecting Convex Figures, Domino Games, Encryption,
Eternity Puzzle, Fair
Dice, Gambling Odds, Graphs, Gravity, Guestbook, Golay
Code, Group Theory, Iamonds,
Knots, Leapers, Locales, Math Software,
Mini-Go, Multistate Mazes,
Number Fun, Parity,
Partridge Puzzle, Path
Problems, Pentagon Tiling, Philosopher Logic, Phonetic
Alphabet, Polyominoes, Prize Page,
Programs, Repeating
Decimals, Retrograde Analysis, Silly Puzzle, Similar
Dissections, Superflu, Stability of the Atom, Riemann Hypothesis, Tic
Tac Toe, Triangles, WGE123, Word Play, World Puzzle Championshiop 2000, Zome.
 |
 |
|
|
  |
 |
Martin Gardner celebrates math puzzles and Mathematical Recreations. This site aims to do the same. If you've made a good, new math puzzle, send it to ed@mathpuzzle.com. My mail address is Ed Pegg Jr, 1607 Park Haven, Champaign, IL 61820. You can join my moderated recreational mathematics email list at http://groups.yahoo.com/group/mathpuzzle/. Other math mailing lists can be found here.
All material on this site is copyright 1998-2004
by Ed Pegg Jr.
Copyrights of submitted materials stays with the contributor and is
used with permission.
 visitors since I started keep track. Yes, over one million.
visitors since I started keep track. Yes, over one million.