material added 4 December 2001

I've added various problems to my Unsolved Problems page. Attacking Queens is $300 contest question by Mike Ecker, who is asking for optimal arrangements of non-attacking queens in higher dimensions. The local paper here wrote an article about the Mathworld case. Particleadventures.org has made some updates, and their little blue book makes a great free stocking stuffer. Alexandre Stefanov maintains a good list of Online Math Books. Naoki Sato points out a nice applet involving pentagons.

Joker Games has released the extremely nice Paso Doble. You control a puppet that must always take two steps. Very interesting.

In response to the Don Woods puzzle, Bob Kraus has created an Eight Question Test: Answer each of the 8 questions with a letter from A to D. The word "answer" in the test refers to YOUR answer, not some "best" answer. Your score is the number of correct answers. Try to get the highest possible score. Answers.

Brendan Owen found, in base-5, 2! 3! 4! 0! 3! = 23403. He found a smaller base-5 example with 4 digits. Can you find it?

Brendan Owen: I haven't found any examples in base 10 where [a1][a2]...[aN] = a1!a2!...aN! (ignoring 1! = 1 and 2! = 2). For bases 2, 3 or 4 I can prove there are no examples. Below are some I have for other bases. I wouldn't be surprised if the examples below were all of them. As the chance of finding them decreases as the base increases. The chance also decreases as the number of digits increase.
Base 5: ????, 23403, 312433,44212310434, 24424322102302443103343312440334244404123,
Base 6: 40, 2544000,
Base 7: 6111015504, 50342420334, 36404240330324160322611, 23055015100142333021661621212352404456062002234, 120220333423556562510105114265634460420501130223040003114,
Base 8: 41600, 2460720000,
377547452334524640060060351754066174725570310360000000000000000000000000000000000,
15070137031640362252356367775365617717052430216234000000000000000000000000000000000,
Base 9: 31347636210421557400000000, Base 11: 33, Base 12: 7360000, 397289a80a800000000000000000,
Base 15: 6ecce600, Base 16: 127500, Base 17: 2e, 12fe, Base 18: d60, Base 20: 14, 1g0, Base 21: 35c,
Base 22: 24, 5a, 144, 1ag, g50c, Base 24: 50, 160, hc0

I recently picked up Sort 1.2 for my PDA. You can see it with the Palm OS Emulator. A java version of much the same thing is at the Sorting Algorithms page. I perused Art of Computer Programming: Sorting and Searching, and was very surprised by the list of best known sorting techniques. The following is a list of commands that show how 9 items can be sorted with 25 comparison-swaps:

Swapper[in_, {i_, j_}] := Block[{out = in}, out[[{i, j}]] = Sort[out[[{i, j}]]]; out];
Sorter[mylist_List,pairs_List] := Fold[Swapper,mylist,pairs];
nine25 = {{1,2}, {4,5}, {7,8}, {2,3}, {5,6}, {8,9}, {1,2}, {4,5}, {7,8}, {1,4}, {4,7}, {1,4},
   {2,5}, {5,8}, {2,5}, {3,6}, {6,9}, {3,6}, {2,4}, {6,8}, {3,7}, {5,7}, {3,5}, {3,4}, {6,7}};
onesandzeros[num_Integer] := Table[Drop[IntegerDigits[2^num + n,2],1],{n,0,2^num - 1}];
Union[Map[Sorter[#,nine25]&,onesandzeros[9]]]

{{0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,1}, {0,0,0,0,0,0,0,1,1}, {0,0,0,0,0,0,1,1,1}, {0,0,0,0,0,1,1,1,1},
  {0,0,0,0,1,1,1,1,1}, {0,0,0,1,1,1,1,1,1}, {0,0,1,1,1,1,1,1,1}, {0,1,1,1,1,1,1,1,1}, {1,1,1,1,1,1,1,1,1}}

I used the "zero-one principle" to prove the nine25 list was valid: If a network with n input lines sorts all 2^n sequences of 0s and 1s into nondecreasing order, it will sort any arbitrary sequence of n numbers into non-decreasing order. I used Mathematica to construct all 512 sequences, and then used the Sorter routine to sort them all. This network for 9 terms was found by R. W. Floyd in 1964, and has not been proven optimal. The last effort to prove optimal sort sequences stopped at 8 terms in 1966. No results above 8 have been proven! Here is the Best Known list. The Batcher Method is the best currently known for 17 and up.

I was curious about the importance of each swap in the Floyd list, so I set qq to the sorted lists, and did this:
Table[Length[Flatten[Map[Position[Map[Sorter[#, Drop[nine25, {n}]] &, onesandzeros[9]], #] &,
Complement[Union[Map[Sorter[#, Drop[nine25, {n}]] &, onesandzeros[9]]], qq]]]], {n, 1, 25}]

{13, 13, 13, 42, 42, 42, 13, 13, 13, 31, 69, 7, 46, 156, 46, 7, 63, 31, 54, 54, 108, 27, 27, 54, 54}

So only 7 sequences don't get sorted correctly when the 12th term {1,4} is dropped. Hughes Juille, in 1995, found a 45-swap method for 13 items, using a computer program simulating an evolutionary process of genetic breeding. If you can improve or prove any of the sorting techniques, write me.

material added 26 November 2001

Although it has a Petersen minor, the Coxeter graph is still 3-colorable. The trick is to find two 14-cycles, which isn't easy. I toyed around with various presentations. Jim Boyce and Joseph DeVincentis sent solutions.

I've moved images and commentary to my new Sam Loyd page. A portfolio of John Whiting's art mazes is at knottedlines.com. Patrick Hamlyn demonstrates that the hexacubes and a 2x2 block can make a size 10 cube in a lot of ways (available at Kadon).

material added 19 November 2001

Many people know of the Four Color Theorem. Less known is the Edge Coloring Theorem. Tait, 1880: The edges of a bridgeless cubic planar graph are three-colorable. A bridged graph () is not three-colorable. A cubic graph is one where each vertex has three edges. Three-colorable means that no two edges of the same color touch. The proof is easy. First, four-color the map. This can be done via the Four Color Theorem. Next, color cyan any edge between red and blue regions, or between yellow and green regions. Color orange any edge between red and green regions, or between blue and yellow regions. Color magenta any edge between red and yellow regions, or between blue and green regions. That's it -- you now have a 3-colored edge coloring.

If you have an edge-colored map, finding the 4 coloring is just as easy. Remove one of the three colors -- magenta, for example. You are left with various closed cycles that connect every vertex. Each region will have an even or odd number of fences around it. Shade the odd-fenced regions red. Next, do the same thing with a different edge color, like orange. Shade the odd-fenced regions yellow. Overlay the two pictures, and you get a four-coloring in red, yellow, orange, and white. Of course, it might not be easy to find the initial 4-coloring. In 1976, Haken and Appel needed a computer to 4-color the following hardest-case map, which I present in a slightly different form.

The 3-edge-coloring is known as the Tait-coloring. In 1884, Tait conjectured that every polyhedra (or 3-connected planar graph) has a Hamiltonian cycle. If true, the 4 color theorem follows immediately. A given map can be made cubic by drawing small circles around each vertex with degree greater than 3, and replacing the vertex with the polygon formed by the intersections. The number of nodes in a cubic graph is even, since the number of edges (vertices * 3/2) must be an integer. For a Tait-coloring, just find the hamiltonian cycle, alternate the colors in the cycle, and draw all remaining edges with the third color. From this edge-coloring, the 4-coloring follows immediately, as shown above. A beautiful idea, but it doesn't work!

Bill Tutte was one of the mathematicians that cracked nazi codes. In 1946, he started thinking that Tait's conjecture might be wrong (here's a link to Tutte's exciting lecture). Eventually, he found the counterexample that is 4-colored above. It is nonhamiltonian, and is thus a counterexample to Tait's conjecture. One counterexample is enough to prove that a conjecture is false.

Tait colorings are still interesting, though. For awhile, only one cubic graph was known that could not be Tait-colored: the famous Petersen graph. Graphs which could not be Tait-colored were called Snarks by Martin Gardner, since like the Lewis Carroll beastie, they were hard to find. Snark pictures.

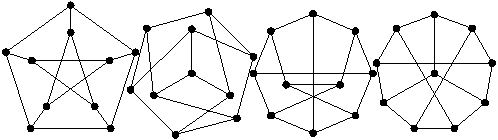
The Petersen Graph (all of these graphs are isomorphic)

In 1966, Tutte noticed that all snarks were related to the Petersen graph, and made the remarkable Tutte conjecture: Any Petersen-free bridgeless cubic graph has a Tait-coloring. Petersen-free means that a Petersen graph cannot be reached by deleting and/or contracting edges (a minor). Note that the word "planar" is not mentioned. The 4 color theorem follows as a consequence, since all planar graphs are Petersen-free.

In 2001, Robertson, Sanders, Seymour and Thomas found a proof of Tutte's conjecture! The same team found the improved 1996 proof of the four color theorem, but that can now be consider a mere warm-up exercise - the Tutte conjecture required over 2000 different unavoidable graphs, and more discharging rules than 4CT.

The below graph is the Coxeter graph. It is non-planar, non-Hamiltonian, and symmetric, according to the Foster Census. For my math puzzle of the week, can this graph be Tait-colored? Or does it have a Petersen minor? Is this a Snark? Send Answer.

Patent 6309716 has been granted to me and Adrian Fisher for the Mitre Tile system, and for Chaos Tiles. Woo-hoo! You can get my Chaos Tiles game from Cleverwood.com (makes a great gift, but I might be biased). My own personal stock, for wholesale orders, is down to 12 cases. Once these are gone, they're gone. At the official Mitre Tile site, you can see some of the marvelous things Adrian has been building with it.

A game of 6x6 go has been given extensive commentary. I'll add more to the above. Astute readers might guess I'll be talking about Hamiltonian cycles. Puzzles.com has noticed some amazing links I should have posted first (especially HexaRoll and Y-Solitaire).

Erich Friedman: I find it interesting that 1! 10! 22! 1! = 11! 0! 2! 21! . The same digits broken up two different ways into factorials. I think this is the smallest such example, but there must be many others. I've been looking for a number that is the product of the factorials of its digits. Can anybody find one? Send Answer.

Jim Boyce and Bob Bosch wrote to me about Set and Superset. Bob pointed me to his marvelous "Mind Sharpeners" column in Optima. For Set, it was issue 63, but every issue is worth a look.

material added 12 November 2001

Robert Heike spent 4 years developing a secret code, and used it in an attempt to break out of prison. Deputy Debra Wesley of St. Lucie's Sheriff department spent 90 minutes cracking it. Here is Heike's letter. Here is the press story. It's a very easy substitution cipher. Can you solve it in less time? Answer.

Brian Tung has been doing an Astronomy version of Mathematical Games. His Pleiadatlas program is very good, too.

Eric Weisstein (another astronomer) pointed me to the Bowl of Integers, as something new at Mathworld. He's gotten over a thousand emails since the return, and is very appreciative to all.

A well-known puzzle involves the game of Set. What is the largest set of cards with no Set? The answer is at the Set site. A variant of Set by Wei-Hwa Huang is Superset. What is the largest set of cards with no Superset? Send Answer. While playing around with a deck of cards numbered 1 to 60, I started looking for subsets of three with a constant difference, like 1 7 13 (difference 6) or 4 27 50 (difference 23). What is the largest set of these cards (1 to 60) that has no such subset? Send Answer.

material added 6 November 2001 (with Nov 7 tweaks)

MATHWORLD IS BACK!!

I'm still working on a puzzle involving special graphs of low diameter. Maybe later tonight. Hey, now I can point you at Eric's listing for the Coxeter Graph! And many other wonderful things.

The above object is a rather special graph. Pick any two node numbers. I claim that I'll be able to connect them with at most four other nodes. For example 1 and 10. {1, 43, 44, 8, 9, 10}. The distance between 1 and 10 is 5. If you look at all the shortest paths between every set of nodes, the longest such path is the Diameter of the graph. The above graph has an amazingly low diameter.

I found the above graph at The Foster Census. Sixty is a nice number, so I'm pondering what sorts of card games could be built with it. But then, I found The (Degree,Diameter) Problem for Graphs -- a page devoted to low diameter graphs. I'm working on getting pictures of the big graphs, using Mathematica. The graph below is the largest one know with a diameter of 4

I've been trying to get a picture for the 70 node graph, but haven't figured it out, yet. I've also spent a few hours trying to find a nicer representation of F60, above. It should have a more symmetrical representation, but I haven't found it. I haven't perfected an F60 card game either.

Puzzlecraft has added a very nice line of puzzles for the collector. If you want to give something very nice to a puzzle loving friend, you need look no farther than here, or Kadon Enterprises, or Cleverwood, unless they don't have Zillions of Games or The Mathematical Explorer.

I put together answers I've received for 20 Questions and the 52 Card Trick.

Ted Drange is a Dan-level go player, and a master of small go games. I met him through NOST (kNights Of the Square Table). "Bill Spight pointed out to me that the alleged canonical sequence that I give for 6x6 go (in the "Mini-go" essay on the Mathpuzzle.com page) is defective. By proper play, White could cut Black's win to only 1 point, instead of 4 points, starting at move #20, but Black could thwart that by playing differently at move #15. An improved (and I think the correct canonical) sequence is as follows:

1-D3, 2-C4, 3-D4, 4-C3, 5-D2, 6-C5, 7-B2, 8-D5, 9-B3, 10-C2, 11-C1, 12-E4, 13-E3, 14-F4, 15-F3, 16-E6, 17-B4, 18-B5, 19-A5, 20-E1, 21-D1, 22-A4, 23-A3x1, 24-B1, 25-A1x1, 26-F2, 27-B1, 28-B6, 29-E2, 30-A6, 31-F1x2, 32-A4x1, 33-F5, 34-E5, 35-B5x1, 36-pass, 37-A4. [37 moves on a 36-point board!] Score: Black 20, White 16. (I've also fixed his email address on the Mini-go page) .

Adrian Fisher sent me a report on unusual mathematical architecture he knew about.

Some Triangular Buildings and Structures by Adrian Fisher

The equilateral triangle is widely found in historic buildings and structures across Europe.

In England there is a famous and unique Triangular Lodge at Rushton inNorthamptonshire. It was built in 1593 by Sir Thomas Tresham as anexpression of his Christian faith, and everywhere the number 3 is used tosymbolize the Trinity (three-in-one: God the Father, Son and Holy Spirit).The groundplan of the lodge is a perfect equilateral triangle, with eachside 33 feet long (by tradition the age of Christ at his death). It hasthree floors, each floor has three windows, and every window is a three-foldTrefoil. There are three gables on each side, and 9 gargoyles. Even thecentral chimney is 3-sided. It must be more than fifty feet tall (maybe 66feet!), and so this is a very substantial stone and brick building. I visited it a few weeks ago and it was very impressive.

There is a triangular castle at Gripsholm in Sweden; part of the Chateau deChantilly in France is entirely based on an equilateral plan, on a gigantic scale. Longford Castle near Odstock was built as a house in the late 16th century and has an unusual triangular floor plan.

During the 18th century, several Folly Towers with triangular foundations were built in England. The triangle provided a more cost-effective way of achieving maximum height for what were, after all, essentially “use-less” structures. These included Fort Belvedere in Windsor Great Park, the triangular sham church on the Cotehele estate in Cornwall, and the Horton Tower known as Sturt’s Folly at Horton, Dorset.

The former hedge maze at Arley Hall in Cheshire, whilst hexagonal in outline, had an internal path geometry based on equilateral triangles; I discovered this when seeking the most effective way of portraying its design
using a computer.

Approached up the only road with a hairpin bend in the Netherlands (everywhere else is too flat!), Three Lands Point is the highest point in the country, and the place where the borders of Germany, Belgium and the Netherlands meet. Here in 1991, I created a giant hornbeam hedge maze 300 feet across, with three distinctive pointed corners to its design, a central triangular goal, three bridges, and 9 Foaming Fountain Gates. There is a colour maze in the courtyard based on equilateral triangles, using the flags of these three nations, each of which is portrayed by a flag containing three stripes of different colours. Paths of three different colours are used to solve this colour maze.

material added 30 October 2001

Is your name in the first 4 billion digits of Pi? At http://pi.nersc.gov/, you can find out. I found "riddles" in Pi, but not "puzzle".

When I was 12 years old, I saw supermagnets mentioned in the Edmund Scientific catalog. I saved up some money and bought one - a samarium cobalt -- the strongest one I could afford. It arrived shortly before my family left for a store, so I opened the box in the back of our 1970 Country Squire station wagon. I experimentally started touching it to a steel plate in the back of the car. Wham! My fingers were suddenly bashed and bleeding, and the magnet was stuck there. My dad asked if anything was wrong. "Nothing," I think I said, in a lot of pain and shame. Still, I love magnetism, and I did exploration with magnets this weekend. I levitated a piece of pyrolytic graphite after seeing the experiment at www.scitoys.com. Levitation is a lot of fun. I learned more as I searched around. Here is a page describing levitated frogs, and levitated sumo wrestlers. I picked up the graphite at Scitoys. For the magnets, I finally opted for http://www.wondermagnets.com/. They have pictures, good prices, good links, and good warning messages. No matter what age you are, get one of the smaller magnets first, so that you can appreciate their power. The Magnet Man site has a lot of good material. Another product I like, for $5, is the set of minimagnets.

The triangulated building has been tracked down. See www.federationsquare.com.au. Thanks to David Eppstein and Khalad Karim for tracking it down, and to Dick Hess for the original pictures. If you know of any mathematical architecture, send it to me or David.

Dick Hess related the following trick: A mathemagician has an audience select five numbers from the set {1,2,3...n}. He thinks carefully about the numbers and then names four of the numbers and asks an audience member to write those four numbers in that order on a blackboard. (The audience contains no shills who might collude with the mathemagician). The mathemagician then leaves the room and a partner who has not seen or heard the proceedings so far is summoned to enter the room (without any contact with the mathemagician). She studies the four numbers on the board and correctly announces the fifth number from the original collection.

Comment: This has been discussed in several mathematical forums in recent years; there are several known solutions for n=52 (I know of two, one being handed out at G4G4 by Colm Mulcahy under the heading "Fitch Cheney's Five Card Trick"). Considerable ingenuity is required to come up with a practical scheme for the maximum value of n and the only known solution requires some practice if your goal is to perform the trick. (I neither know the maximum value for n for which the trick can be performed nor do I know of any method for n>52). 52 Card Trick Solutions

Simple permutations, ranking the cards from lowest to highest, will get to n=24. {{1,2,3,4}, {1,2,4,3}, {1,3,2,4}, {1,3,4,2}, {1,4,2,3}, {1,4,3,2}, {2,1,3,4}, {2,1,4,3}, {2,3,1,4}, {2,3,4,1}, {2,4,1,3}, {2,4,3,1}, {3,1,2,4}, {3,1,4,2}, {3,2,1,4}, {3,2,4,1}, {3,4,1,2}, {3,4,2,1}, {4,1,2,3}, {4,1,3,2}, {4,2,1,3}, {4,2,3,1}, {4,3,1,2}, {4,3,2,1}}.

Alec Mihailovs runs a good problem of the week at Shepherd college.

material added 22 October 2001

I recently had two nice articles pointed out to me. David Singmaster's Essay on Recreational Mathematics. An interview with Martin Gardner.

Bill Cutler has written a program that can solve my Kites & Bricks puzzle (I still have a few available, at $15 each). It turns out it has exactly 5 solutions. Koshi Arai and his solving group found all five by hand about a year ago. Bill checked the desirable 7-7-7 case for me, and it turns out there are no solutions for it.

I was watching the TV show Alias on Sunday night (I like it), and was surprised when it was revealed that Kate Jones was some sort of mastermind international spy. She is certainly a puzzle mastermind, I'll vouch for that. Kate runs Gamepuzzles.com, which is the best toy store around for unusual puzzle gifts. Here is her article on naming the 166 hexomino pieces. Another good place to shop is Cleverwood.com -- Kathleen Malcolmson can't claim to be an international spy, but she did make some incredible deals while she was in Japan. She can now offer high quality puzzle boxes at even lower prices.

Dave Tuller, a regular contributor here, and the author of Mensa Math and Logic Puzzles, helped to design puzzles for the truly bizarre Nemesis Factor.

While looking up some things about polyhedral graphs, I found the Symmetry page of Steven Dutch.

The 40 cubes puzzle had a mistake! It was solved by Denis Borris, Clinton Weaver and Jeffrey Smith. The typo was the k and K in lines 6 and 7. I give the corrected version below. (apologies for that).

FORTY CUBES by Rhombus

Koshi Arai, Mark Michell, Claudio Baiocchi, Clinton Weaver, Liu Wei, Juha Saukkola, and Joseph DeVincentis all solved my 17x17 domino-tromino problem. Guenter Stertenbrink's program found sequential domino-tromino dissections of the following rectangles: 2*5, 2*7, 7*10, 9*15, 10*12, 12*16, 14*14, 14*21, 14*31, 17*17, 24*29. He also created these problems: "Divide a 20x20 square into 11 different dominoes and trominoes. Divide a 17x17 square into 9 different dominoes and trominoes." Send answers. These are my favorite types of problems - something short that I can remember and solve when I have time.

material added 14 October 2001

From Erich Friedman -- cut a 20x20 square into 14 smaller squares so that the biggest subsquare cannot be placed in the corner.

I started looking for possible variants on this. Let a Domino be a n×2n rectangle, and a Tromino be a n×3n rectangle. If you represent the series 1 to 6 with dominoes and trominoes, can a 14×14 square be made with the 6 pieces? Yes, it can. The solution is below. If you represent the series 1 to 7 with dominoes and trominoes, can a 17×17 square be made with the 7 pieces? Yes, it can. A nice little puzzle.What is the next square that can be covered with a sequential series of dominoes and trominoes? I don't know, yet. Send Answers.

I had the pleasure of attending the Mathematica Developer's Conference. A couple of things I saw there were functions.wolfram.com and polytopes.wolfram.com -- two excellent resources. You can also peruse some web-mathematica items.

Nick Baxter has posted results of the 2001 World Puzzle Championship.

Melkor-Bradley has some interesting games for sale. The 916 test is well worth a look. For retrograde analysis, be sure to visit the Dead Reckoning page.

material added 6 October 2001

Lloyd King sent me a nice little puzzle he calls Die-Hard. Arrange the six equilateral triangles to create a view of a regular die. If you can figure out the numbers on the die, write me. For another puzzle with dice, see Andy Brown's Puzzlemaniac site (he also does dominoes and signal towers).

Die-Hard puzzle by Lloyd King

Eric Weisstein and I recently had the pleasure of hearing Clark Kimberling give a lecture on triangles. You can get a taste of this at the Encyclopedia of Triangle Centers website (ETC). I've now been studying the mathematics of trilinears for several days now.

Part of the Slocum Puzzle Foundation Collection will be shown in the Lilly Library at Indiana University Bloomington from October 11 to December 18, 2001. Here are more details. Here's a map (from MapQuest.com). I live in Champaign-Urbana, in the upper left. I'll try to visit there October 20th. In related puzzle news, John Rausch has updated Puzzle World.

Erich Friedman's Math Magic this month is about entangled polyforms. Chris Lusby Taylor has improved the Picture Hanging solution. Koshi sent me a picture from my visit to Tokyo. I'm in the Mathematica T-shirt. A lot of people have wondered what I look like.

John Gowland wonders if the puzzles of Rhombus have been collected anywhere. Rhombus is his favorite cross number constructor. He sent me the following puzzle by Rhombus, as a sample. Forty Cubes is his all-time favorite.

I have a small supply of Kites & Bricks puzzles available. There were cut by Walter Hoppe (he does incredible work). You can see the wooden version at the Puzzle Design Competition. If you'd like to order one of them (for $15), please write me.

I've become a big fan of Ken Krugler's Turmite program. As soon as I find a few extra minutes of spare time, I'll show Turmites discovered by Ken and myself. In the meantime, here is my current Palm database file.

material added 30 September 2001

Can anybody pack all 12 pentominoes to a 9x9 square grid, so that any pair of pentominoes share at most one grid segment? That is, two adjacent pentominoes can only touch at one side of one square only. Jukka-Pekka Ikäheimonen found a solution the day after he asked me the question. The image shows only 11 pieces. Can you find JP's answer? This problem was solved by Andy Brown, Matthew Prins, Jukka-Pekka Ikäheimonen, Clint Weaver, Koshi Arai, Juha Saukkola, Livio Zucca.

Samantha Levin, Denis Borris ("Boy, Ed: what a beautiful challenging puzzle."), Jeffrey D. Smith ("The puzzle was really good, so I hunted and found another that you had posted on your site."), Bob Kraus ("a nice puzzle of its type"), and Joseph DeVincentis ("I liked this puzzle.") solved John Gowland's Four of a Kind problem (here's the answer). Several people have asked me if I know of other places with cross-number problems. One of them is at Arik Schenkler's site, at internetdollar.com. Neil Fitzgerald solved the Hanging a Picture problem. Torsten Sillke kindly sent me some history of this nice problem. (Write-ups)

material added 24 September 2001

It is possible to hang a painting with two nails so that removing either of them will cause the picture to fall. Here's how to do it. John Lawton found that this can be done with any number of nails (remove one, and the painting falls). Can you see how to do it with five or six nails? Answer.

I recently picked up a cheap Palm Pilot (a Handspring, actually). These have gotten more powerful than I realized. One nice application for it is a Wordplay program by NPL member Kiran Kedlaya. I found a very nice "turmite" program for the Palm OS ( Turmite1.0b ). A Windows version is at Kasprzyk's ALife Page. A Linux version is call Ants and is included with the Gnome packages.

Stan Wagon, in the latest MacPOW, notes there are exactly 13 unlucky numbers 2, 3, 5, 6, 7, 8, 12, 13, 14, 15, 19, 21, and 23. A lucky number is one that can be partitioned so that the sum of its reciprocals is exactly 1. For example, 11 = 2+3+6 is a partition of 11 with the reciprocals of the terms summing to 1. He created algorithm that can find all the lucky partitions of 60 in less than 4 seconds, and challenges others to do likewise. (Out of curiousity, how many of my readers have picked up Stan Wagon's The Mathematical Explorer? Please write me with your thoughts about it, and I'll send you something interesting. Don't miss it at the introductory price of $70.)

Brendan Owen has found that polykites of order 1-5 will make a perfect triangle. See his page about them. Oli Donald pointed out HAKMEM to me, which has a lot of neat stuff. On polyforms, N J A Sloane would like a better explanation of polyform types.

John Gowland sent me a new logic puzzle. In this crossnumber, p and q are three digit primes whose product is a 5 digit number, which can be considered as a "four of a kind" in a poker hand. e.g. 113 x 823 = 92999. This product is clued as a 3-digit number r according to the following convention: A number in the form 12222 will be clued as 122; a number in the form 11112 will be clued as 112; and numbers in the form 12111, 11211, or 11121 will all be clued as 121. Across entries are denoted by capitals and down entries are denoted by small letters. There are no zeroes in the completed diagram. Answer.

Brendan Owen and Patrick Hamlyn put together the following checkered octiamond solution:

material added 15 September 2001

I met Brendan Owen via Christopher Monckton and the Eternity Puzzle. This was a spectacular risk on Christopher's part, to make a fair puzzle that gave a million pounds to the first solver. It led to new refinement of the Breadth First Search algorithm, which will be of major importance eventually. Brendan was part of the research team known as the Eternity Mailing List.

Brendan, an Australian, hurt his foot while rock climbing four years ago. Early this year, while visiting the UK, he got a very bad infection in his foot. His father looked through Brendan's email and noticed that Martin Watson lived near the hospital, and contacted him. I spoke with Martin while I was in Tokyo. For several weeks, Martin visited Brendan at the hospital. Now, Brendan has mostly recovered, but needs to keep his leg elevated 95% of the time, which means a lot of time at the computer.

On Thursday, Brendan solved my longstanding checkered octiamond problem (above).

The mighty RetroAnalysis Corner is now at janko.at/Retros/index.htm. There is a free International Phonetic Alphabet at www.cascadilla.com/eyechart.html.

Adrian Fisher collects books on interesting architecture, and here's one that sounds fascinating: "Castel del Monte, Geometric Marvel of the Middle Ages" by Heinz Gotze, published by Prestel, Munich and New York, in 1998; ISBN 3 7913 1930 2. This entire 200 page large format illustrated book is seemingly devoted to a single octagonal castle in Southern Italy. In fact, the astonishing octagonal geometry of this castle is merely the catalyst for a complete celebration of the Octagon and its related geometry, from octagonal Roman mosaics and tiling patterns in the Alhambra Palace in Spain, to Jerusalem's Dome of the Rock, and the Church of San Vitale in Ravenna (which also contains a splendid multi-coloured marble pavement labyrinth). The accuracy of stone craftsmanship of the castle in three dimensions is awesome. The geometry of the Castle itself is astonishing - a central octagonal core containing an inner octagonal courtyard, surrounded by 8 perfectly octagonal towers, all rising to a great height more in the character of a cathedral (or a triumphal palace) than a defensive place of refuge. Certainly the castle remains undamaged to this day, as if it never experienced hostilities." Now that I know the name, I found a lot of info about the castle on the internet.

material added 12 September 2001

Stan Wagon has posted problem of the week 939 to the macpow mailing list : Find 939 distinct positive integers such that for every seven of them, their product is divisible by their sum. The answer to Andy Liu's Lion and Lamb problem was also posted.

Juha Saukkola, Joseph DeVincentis, and Don Woods found the distribution of Urns that will cover all possible distributions of draws: 001122, 000012, 111102, 222201. Robert Jenkins has a score of 18 on the Don Woods challenge.

On Monday, I received a Polymorf set. It's a very good set, and reasonably priced. I like Zome, too, but Polymorf allows an easy study of polyhedral nets. Fascinating.

material added 11 September 2001 -- Addendum

Nothing can stop the wonder of mathematics. It has survived time, war, attacks, and disasters. St. Andrew lists the following about Archimedes.

The problem was more important than the war, to Archimedes. Today, he and his work are still revered. St. Andrews has many such stories of mathematicians. Sophus Lie made some of his greatest discoveries while in prison, suspected of being a spy. During my last visit with Stephen Wolfram, we pulled out an older book of Integral tables as a reference, and it turned out to have been the possession of a WWII German prisoner-of-war in a US camp. Adrian Fisher, a maze maker and my friend, lives on a street that was heavily bombed during that war. Nob Yoshigahara, a survivor of both a large chemical explosion and cancer, is one of the great puzzle creators and ambassabors. He personally welcomed me to Japan. Vladeta Jovovic, a programmer from Belgrade, Yugoslavia, sent me a nice recreational math program while his country was getting bombed by mine.

I spent some of the day working on a diagram of Stephen's based on Euclid's Elements. This was a favorite book of Abraham Lincoln, who memorized many of the proofs. One of my co-workers pointed out that the image I posted earlier today was very similar to Voronoi diagrams. I met Eric Weisstein's father, and showed him a puzzle based on one of Eric's diagrams.

material added 2 September 2001

The entries for the first International Puzzle Party Design Competition have been put together by Nick Baxter. There are many excellent puzzles here, of course. Of particular mathematical interest are ... oh ... half of them. Many of the puzzles are quite affordable. As a puzzle for here, Nick would like you to look at the Yosegi puzzle. It consists of 32 half-square right triangles. 16 of them are light-dark-light, and 16 are dark-light-dark. Nick's puzzle: How many designs are possible? Slightly harder: How many designs are possible without similar colors touching? Send answer.

Roger Phillips has sent me a way to tile a 7x7 torus with 7 heptominos so that they all touch each other. In fact, he sent me 18 different solutions. He also found 22 different hexominoes that will cover a 6x6 square, so that all touch each other. Here's an image suitable for wallpaper. Mark Thompson, Guenter Stertenbrink, and Roel Huisman also worked on this problem.

Dan Blum and Jim Boyce found that 4 urns is enough for Don Woods problem below. Can you find the distribution? Send Answer. Robert Jenkins has managed to get a score of 18 on the Don Woods challenge.

Adrian Fisher has built a maze with double decker bridges. Livio Zucca has a new polymultiform update.

Stan Wagon has posted the latest Macalester College Problem of the Week. This time, its a nice one by Andy Liu.

An immense ammount of good stuff is available at www.g4g4.com, including a full book.

Marcel Tuenissen and Ramon van der Winkel have examined Dr. Wood's iamond problem (way at the bottom). The found there are exactly 2035428 ways to fill this shape with the checkered hexiamonds. My own puzzle: If the Octiamonds are checkered in all possible ways, you wind up with 225 pieces.  Can they make a side-30 checkered diamond?

A pretty proof of mine. I know Alexander Soifer published this in the USSR many years ago, whilst still a lad. The problem: the sides of a triangle are trisected, and lines are drawn from the corners to three of the trisection marks. What is the area of the internal triangle that is created, compared with the original triangle?

material added 26 August 2001

Don Woods, one of the creators of the original Adventure game, has kindly sent me his new Twenty Questions puzzle. Send Answer. He constructed it after seeing Jim Propp's Self-Refential Aptitude test. Don also described a different puzzle he is working on. Let T be the the number of object types (if T=3, there are 3 types of object), and let D be the number of objects that can be drawn (If D=4, you will draw 4 objects). In the case T=3, D=4, the possible draws are: 0000, 0001, 0002, 0011, 0012, 0022, 0111, 0112, 0122, 0222, 1111, 1112, 1122, 1222, and 2222. Let U be number of objects an Urn can hold. Suppose that U=6. You need at least 5 urns to cover all possible draws: 011112, 112222, 001222, 000112, and 000022 will do. Can anyone find a method for finding the number of Urns required to cover all possible draws, given T, D and U? This is related to items in the La Jolla Covering Repository, but is a different problem.

A photo by Dick Hess, taken in Melbourne (Flinders street). Same idea as Kites & Bricks.

Paul Nahay has made his Septangle puzzle available as a java applet.

Oriel Maxime shows how a simple packing problem can become NP-complete.

A few good places to shop for puzzles: puzzleman.com, kubi-games.de and hras.cz .

Al Stanger, Don Woods, Bob Henderson, Jim Boyce, James Lewis Melby, Joseph DeVincentis, Chris Lusby Taylor, Dick Saunders Jr, Dane Brooke, Doug Orleans, Hugh Rutherford, Nathan Stohler, and Franjo Schulte all sent solutions to the magic square of small fractions. With the conditions as stated, and eliminating rotations and reflections, the solution is unique. The below is Don Woods' method:

  8 1 6   -5 13  4          1/6 7/9 5/9
( 3 5 7 + 13  4 -5 ) / 18 = 8/9 1/2 1/9
  4 9 2    4 -5 13          4/9 2/9 5/6

material added 21 August 2001

The place where I work, Wolfram Research, has launched The Mathematical Explorer (TME). It's a $69 program that contains an interactive book in recreational mathematics by Stan Wagon (a long-time #1 writer on my books page). Mathematica is not needed to run TME. Instead, the TME has a self-contained version of Mathematica with certain high level functions disabled, and new recreational functions added. It does a lot.

material added 19 August 2001

Before landing in Tokyo, I had to fill out a disembarkation form. This was the first time I was able to list my occupation as "Mathematician." I figured out the train system quickly enough. I tried a triangle of sticky rice wrapped in a seaweed paper, and found it was very good. It had tuna at the center for flavoring. Nob Yoshigahara helped me identify other flavors. They were all good, and cost 100 yen (about 80 cents). Nob is letting me share an idea of his. One day, he pondered the dodecahedron. 12 faces. There are 24 ways that 1,2,3,4,5 can be arranged in a circle. Each such circle is a mirror image of one of the others. He put these mirror images on either side of a pentagon, to obtain 12 pentagons. (1+2+3+4+5)*12 = 180 = 9*20. Can these pentagons be arranged so that all 20 corners add up to 9? Nob solved it. The below figure has all 12 permutations of {1 2 3 4 5}, and each corner has a sum of 9. It's neat. Things like this make life more fun.

Oskar van Deventer tried out a more elaborate japanese meal with me and some others. Oscar had several new puzzle creations with him. One of the favorites was his velcro blocks puzzle, that he detailed earlier. This is a great little maze, and quite challenging. It's the next thing I'll make for myself. I bought a copy of his Metro puzzle, and like it a lot. Another puzzle he gave me permission to mention involved a velcro covered icosahedron, and a velcro strip of 23 triangles. The task was to completely cover the icosahedron with the strip. Very nice puzzle, and easy to make. He's examined all the deltahedra and zonohedra as well

Alan Segal, manager of Bits and Pieces, gave me a lovely anodized aluminum burr puzzle. He had a full collection of metal puzzles available there, and I bought one of each. He personally asked me to invite everyone to see the range of metal puzzles he has available. Many of the brass puzzles were designed by Rocky Chiaro. Rocky sold me one of his hand-made brass creations. Others are available at his website. Also looking at metal, I met the owner of a site devoted to ancient chinese locks.

I'll have much more to relate this week.

Jonathan Welton showed me his Y-solitaire idea. I've tried out his javascript version, and really like it.

Martin Gardner has released The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. I'm eager to see the expanded addenda for his 50 favorite columns.